Diminished Java Compiler

Introduction

This article will go over the tools and concepts covered in maybe the hardest yet most rewarding course I have taken in my undergraduate computer science program. The course is simply tilted 'compilers' and is an introductory course for both undergraduates and master students.

I will begin by describing the language we are implementing a compiler for then we will walk through all the stages of compilation until we arrive at our target code.

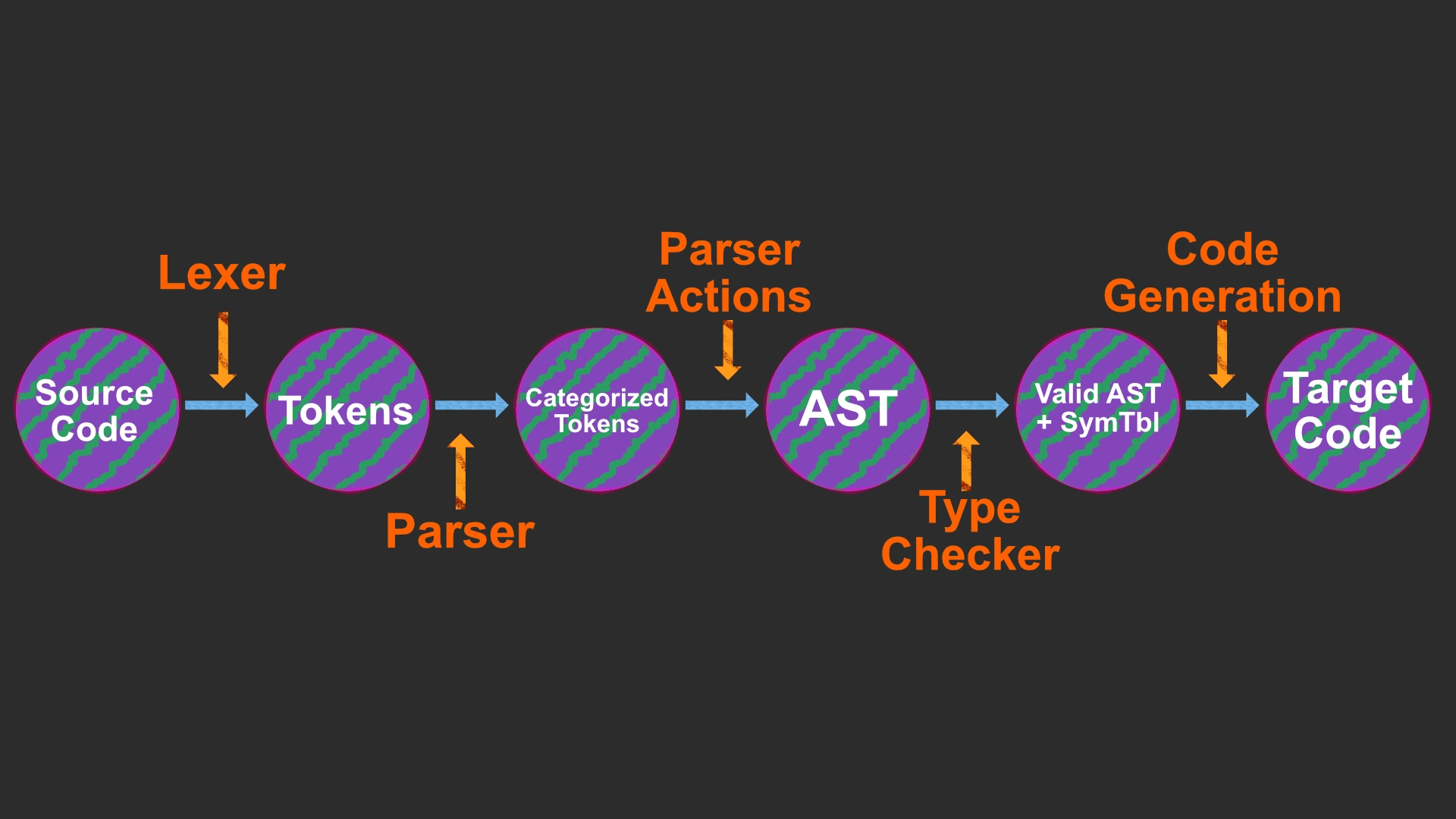
Source Code - What is DJ

Diminished Java (DJ) is a complete object-oriented programming language. DJ is Turing complete, meaning that any Turing machine can be encoded as a DJ program.

While DJ is capable of what standard languages are, in terms of core features, it is still a very simple language. Enough to cover all the phases of the compilation process in one semester.

DJ has the following types:

• nat: a natural number.
• bool: a boolean value i.e. true or false.
• Object: Base class for every user defined class.

Since a Turing machine would not be a turing machine without looping, DJ uses a for loop with the following form:

Expression's make up the power of programming languages. Recursion is what allow us to design and implement these languages. Hence, recursion was used extensively in this project and it was awesome to see how recursion can be used in non-trivial software engineering.

DJ includes logical AND that short circuits, not expressed with the exclamation mark, less than, equality as the double equal sign instead of the walrus operator seen in other languages, and interestingly the 'instanceof' expression. DJ has standard math operations for addition, subtraction, and multiplication.

Now that we have the idea of what we need our language to be capable of, we can begin the first step of compilation and thats turning the source code into tokens.

Lexing

For our compiler we took advantage of the flex (fast lex) program. Flex allows us to write a more user friendly version of a lexer. The alternative, which I chose to do for extra credit, is to hand write the DFA state machine that will match your programs character sequence. Since I had not taken Automata at this point in time, the material was challenging. We learned all about the different categories of languages and what we could and could not use to model them.

The lexer has the responsibility of tokenizing the entire source code. We will then use these tokens and 'feed' them to a parser via a token stream.

Through the use of Deterministic Finite Automata we are able to work through the source code file and for each character try and find the program token it represents.

There are two rules when lexing:

1. Match the character sequence to the longest valid match.
2. If there are two matches of the same length, match the token that is defined first in the flex file's rules section.

Implementing this by hand was actually a very motivating experience because I could see how ideas like Automata could be applied to programs. The program consisted of enumerations, a while loop, and a large switch case. With these simple tools, I was able to create a large state machine. Again, seeing this go from theory to practice in such a short time was so inspiring to me.

A nice feature of Flex is that instead of writing out this giant DFA, we simply write the regular expressions for each program symbol. We can do this because both regular expressions and DFAs are used to define regular languages.

Now that we have our tokens it is time to feed them to the parser.

Parsing

First, let's understand that the parser's job involves analyzing the relationships between tokens according to the rules of a grammar. "Why can we not just do that with the lexer?" one might ask. This is because regular languages, which lexers can handle using regular expressions, lack the ability to manage nested structures or "remember" past inputs beyond a fixed limit. This limitation is particularly crucial when dealing with recursion or nested structures in programming languages.

So, what do we need when we require the ability to handle recursion? A stack.

By integrating a stack into the process, we can utilize a Push-Down Automata (PDA), which is capable of handling context-free grammars. PDAs expand on the capabilities of finite automata (used in lexers) by adding a stack. This stack allows the automaton to handle a broader class of structures by keeping track of a potentially unbounded number of states. This capability is essential for recognizing patterns like nested parentheses or recursive function calls, which are common in programming languages.

This could have been done by hand in C, but we used a tool called Bison instead. Bison is a descendant of yacc (yet another compiler compiler) and serves as a parser generator. It allows us to define our context-free grammar in the Backus-Naur Form (BNF), which simplifies the process significantly.

Besides allowing us to write our CFG, Bison enables us to build our Abstract Syntax Tree (AST) via semantic actions. As the program is parsed through the grammar, we construct a tree data structure that represents our program. This tree acts as the intermediate representation for our compiler. This data structure is what connects the front end of our compiler, which focuses on source code analysis, to the back end, which focuses on synthesis. The goal of the back end is to synthesize the target code.

Thanks to Bison, which facilitates the building of our AST, we are now prepared to ensure that the program is type-safe. To do this, we will pass our AST to generate a symbol table that will enable us to perform type checking.

The AST & Symbol Table

Before we start type checking our program, i.e., enacting memory access control on all program-level values, we need to build our symbol table. The symbol table is responsible for storing information about the scope, binding, and properties of different program identifiers.

In our program, we will maintain a symbol table for the classes and the main block. The symbol table for the classes will hold information regarding static members, non-static members, class methods, parameters, and local variables.

Both symbol tables are built by traversing the AST that our parser constructs. It is important to note that while the symbol table is being built, type checking is not performed. There may be invalid types throughout the table, but it is not the job of the symbol table builder to type check. This distinction is a crucial aspect of maintaining a division of labor.

When we maintain and build software with a separation of labor, we create more robust software. This approach aligns with the goal of having highly cohesive code. Our objective is to take a problem, even something as complex as compiling, and break it down into smaller, manageable problems that can be solved sequentially. Attempting to do everything in one place is prone to errors.

With our symbol tables ready, we can now begin the type checking work.

Type Checking

Our first question is how do we go about type checking? Is this something we can use automata for? Sadly, no. Type checking moves beyond the scope of what can be achieved with push-down automata (PDAs). PDAs handle parsers very well because they are suitable for context-free grammars, which describe the syntax of programming languages without considering the context or meaning of the code. We have now entered an area that is context-sensitive.

What does it mean to be context-sensitive? It means that the correctness of some constructions in the code depends on the context in which they appear. For instance, the type correctness of a variable depends not only on its declaration but also on how it is used throughout the program.

We can see context sensitivity with:

• variable scoping: Where is the variable defined, is it accessible from where it is being used?
• function overloading: Due to polymorphism, functions in child classes may overwrite parent functions. How do we know which function is being called? Is the function being passed the correct argument types?
• type consistency: When we perform mathematical operations, or we are making assignments to variables, are they allowed operations?

Type safety is a growing (for good reason) issue in programming languages. Governments are getting involved and pushing for type safety. We would not want to let some program have a class for Dogs then later down the line assign a number variable to be a dog. It doesn't make sense. While in that trivial example it just seems silly, with careful planning attackers can (and do) take advantage of a weakly typed language and hi-jack memory.

To begin type checking we work through an algorithm that will type check the entire program via the symbol tables. The algorithm is along the lines of the following:

1. Ensure there are no duplicate classes
2. Check that all the values in the table are valid
   • non-object super type is >= 0
   • class type doesn't equal super type
   • all static & non-static members >= -2
   • all method params and return types >= -2
   • all local types are >= -2
3. Check that class hierarchy is acyclic
4. Check that all static and non-static field names are unique in their defining class and superclasses
5. For all methods:
   • check that method name is unique in defining class
   • check that method names with a matching name in a super class have matching signatures
   • method params and locals have no duplicates
   • methods expression list is well typed and returns a subtype of the declared type
6. Check that main block vars has no duplicates
7. Check that method body is well typed and the return type is well typed

While this algorithm does not focus on efficiency it does focus on correctness.

With our program type checked, meaning we have enacted type safety i.e., memory access control, we can begin to generate code.

Code Generation

For our compiler our target code was a RISC like ISA called DISM or Diminished Instruction Set Machine. DISM is comprised of 12 commands including the standard loading and storing, and the ability to print natural numbers and read natural numbers in as featured instructions.

We again begin with our AST and start recursively traversing the AST to generate our program in DISM, which are the instructions a machine can understand and execute.

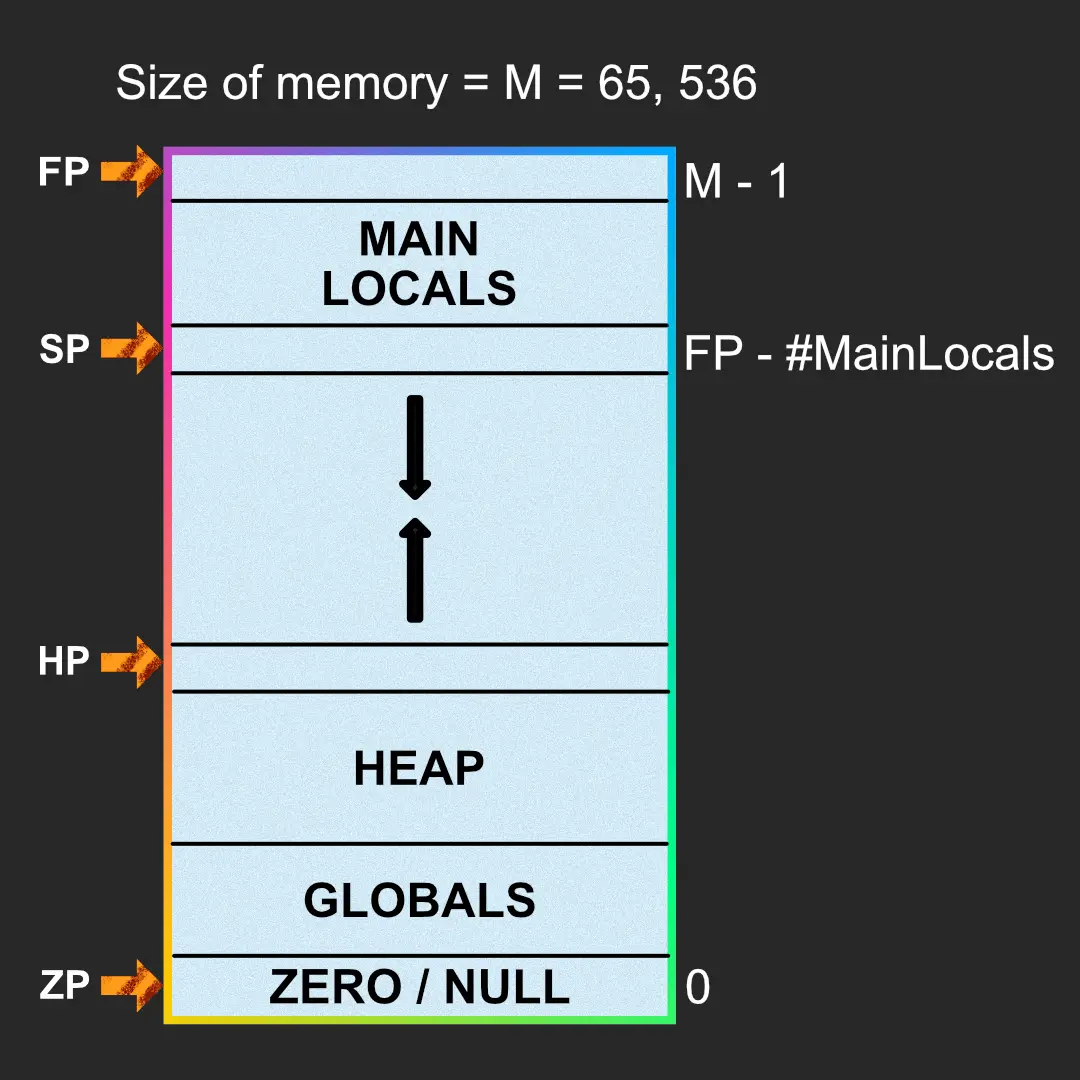
To understand code generation for DJ, we need to understand how we have memory layed out as that determines how our program will work with the machine.

Conclusion

In conclusion, Compilers was probably the most challenging class I have ever taken. The course takes decades of research and theory and brings it all together to implement something non-trivial and in my eyes magical -- a compiler.

After taking this course, I feel more competent as a computer scientist as I have a better understanding of what our programs are doing when we run something like 'gcc'. Not only do I have a understanding our what compilers do, I am able to understand error messages with much more ease. Additionally, I understand how programs layout memory and how they all come together to interact with each other to produce the code that runs much of our society.

By no means does this single course bring me to the depth of modern day compilers and everything that takes place in industry. However, the course gave me all the tools and concepts I need to start a career in compilers and it (in my opinion) has made me a more competent and able computer scientist.